找到
8
篇与
数据分析
相关的结果
- 第 2 页
-
【SPSS】相关性分析 #BV# 若视频不清晰请点此观看原视频 步骤 对变量进行统计： 转化 > 计算变量 目标变量输入维度名称，数字表达式输入mean(维度下第一题 to 维度下最后一题) 例如(题目名称不用手动输入，直接点击左侧对应标签即可)： 对所有维度执行相同操作。 选择分析方法：点击菜单栏的“分析” > “相关” > “双变量”。 选择变量：在弹出的对话框中，将希望分析相关性的变量(通常为所有的量表维度)添加到“变量”框中。 选择相关系数类型：在“相关系数”部分，通常选择“皮尔逊”相关系数。如果数据不满足正态分布，可以选择“斯皮尔曼”或“肯德尔”相关系数。 运行分析：设置完成后，点击“确定”以运行分析。 查看结果：SPSS会在输出窗口中生成相关系数矩阵，包括每对变量之间的相关系数、显著性水平（p值）等信息。通常，p值小于0.05表示相关性显著。 表格：表格绘制为以下样式： 热力图：还可以绘制热力图，使结果更直观、美观： 绘图代码 解读 *：p＜0.05 **：p＜0.01 ***：p＜0.001 Word解释 相关性 绩效期望 努力期望 促进因素 社会影响 感知风险 享乐动机 价格价值 个体创新 使用意愿 绩效期望 1 努力期望 0.712** 1 促进因素 0.687** 0.745** 1 社会影响 0.651** 0.731** 0.817** 1 感知风险 0.451** 0.499** 0.544** 0.602** 1 享乐动机 0.743** 0.701** 0.781** 0.757** 0.570** 1 价格价值 0.646** 0.618** 0.766** 0.691** 0.593** 0.752** 1 个体创新 0.696** 0.745** 0.713** 0.744** 0.589** 0.806** 0.716** 1 使用意愿 0.684** 0.665** 0.801** 0.759** 0.576** 0.782** 0.834** 0.779** 1 当相关系数大于0时正相关，小于0时负相关；当其绝对值小于0.3时无相关性，0.3~0.5时低相关，0.5~0.8时中度相关，大于0.8时高度相关。因此，根据以上表格数据得出结论： 绩效期望与努力期望的相关系数为0.712，P＜0.01，说明两者呈现中度正相关关系； 努力期望与促进因素的相关系数为0.745，P＜0.01，说明两者呈现中度正相关关系； 促进因素与社会影响的相关系数为0.817，P＜0.01，说明两者呈现高度正相关关系； 社会影响与感知风险的相关系数为0.602，P＜0.01，说明两者呈现中度正相关关系； 享乐动机与价格价值的相关系数为0.752，P＜0.01，说明两者呈现中度正相关关系； 个体创新与使用意愿的相关系数为0.779，P＜0.01，说明两者呈现中度正相关关系； 使用意愿与价格价值的相关系数为0.834，P＜0.01，说明两者呈现高度正相关关系。
-
【SPSS】差异分析 #BV# 若视频不清晰请点此观看原视频 数据表达形式 在进行正态性检验时，通常有以下两种数据展示方式： 正态分布数据：使用均值（M）和标准差（SD）来呈现，适用于参数检验（如T检验、ANOVA）。 非正态分布数据：使用中位数和四分位数（IQR）来呈现，适用于非参数检验。 然而，在问卷分析中，大多数情况下仍使用参数检验，并通过均值±标准差（M±SD）来呈现数据。 独立样本T检验：用于二分组变量（如性别：男、女）和连续型因变量（如成绩）之间的比较。 单因素方差分析（ANOVA）：用于多分类变量（因子）和连续型因变量（如成绩）之间的比较。 变量前置操作 转化 > 计算变量 目标变量输入维度名称，数字表达式输入mean(维度下第一题 to 维度下最后一题) 例如(题目名称不用手动输入，直接点击左侧对应标签即可)： 对所有维度执行相同操作。 独立样本T检验 操作步骤 选择分析方法：点击菜单栏的“分析” > “比较均值” > “独立样本T检验”。 设置变量：在弹出的对话框中，将因变量添加到“检验变量”框中，将分组变量添加到“分组变量”框中。点击“定义组”，输入分组变量的取值（如男=1，女=2），然后点击“继续”。 选择选项：点击“选项”按钮，勾选“均值和标准差”以及“显著性水平”，以便输出相关统计量和显著性检验结果。 运行分析：设置完成后，点击“确定”以运行分析。 绘制表格如下： 结果解读 描述统计：查看每组的均值、标准差和样本量。例如，男生的平均成绩为80，女生为85。 方差齐性检验：在“莱文方差等同性检验”表中，查看“显著性”值。如果“显著性”值大于0.05，表示方差齐性假设成立，看“假定等方差”这一行数据；如果小于0.05，表示方差不齐性，看“不假定等方差”这一行数据。例如，Sig.=0.653 > 0.05，说明方差齐性。 T检验结果：在“T检验”表中，查看“Sig.”值。如果“Sig.”值小于0.05，表示两组均值差异显著；如果大于0.05，表示差异不显著。例如，Sig.=0.116 > 0.05，说明差异不显著。 T：t值是由样本数据计算得出的，用于衡量样本均值差异与样本变异性之间的关系 t值越大，说明两组之间的均值差异越大，相对变异性较小，表示组间差异可能较为显著。 t值越小，则表示均值差异较小，可能说明两组之间没有显著差异。 单因素方差分析（ANOVA） 操作步骤 选择分析方法：点击菜单栏的“分析” > “比较均值” > “单因素ANOVA”。 设置变量：在弹出的对话框中，将因变量添加到“因变量列表”框中，将因子添加到“因子”框中。 选择选项：点击“选项”按钮，勾选“描述”。 运行分析：设置完成后，点击“确定”以运行分析。 结果解读 描述统计：查看每组的均值、标准差和样本量。例如，教学方法A的平均成绩为75，B为80，C为85。 ANOVA结果：在“ANOVA”表中，查看“Sig.”值。如果“Sig.”值小于0.05，表示组间均值差异显著；如果大于0.05，表示差异不显著。例如，Sig.=0.116 > 0.05，说明差异不显著。 F值：反映了组间差异与组内差异的比值 补充 如果想进一步分析，可以对有显著差异的变量进行：事后比较——假定等方差中的LSD。 解读： 均值差异（I - J）： 该数值表示两组之间的均值差异。如果为正值，说明第一组（I组）的均值大于第二组（J组）；若为负值，则表示第一组（I组）的均值小于第二组（J组）。 显著性（Sig.）： 如果P值<0.05，说明两组之间的均值差异显著； 如果P值≥0.05，说明差异不显著。 结果展示： 保留的行：因变量、I、J、I-J、显著性 保留的列：P值<0.05的组别 Word解释 独立样本T检验 选项 男 女 T P 绩效期望 3.72 ± 0.92 3.71 ± 0.80 0.109 0.913 努力期望 3.77 ± 0.98 3.89 ± 0.74 -1.148 0.252 促进因素 3.70 ± 0.93 3.78 ± 0.79 -0.776 0.438 社会影响 3.66 ± 0.89 3.79 ± 0.75 -1.289 0.199 感知风险 3.70 ± 0.93 3.83 ± 0.79 -1.236 0.218 享乐动机 3.66 ± 0.94 3.66 ± 0.80 -0.038 0.970 价格价值 3.57 ± 0.91 3.36 ± 0.79 2.007 0.046 个体创新 3.88 ± 0.89 3.78 ± 0.75 0.930 0.353 使用意愿 3.65 ± 0.90 3.51 ± 0.82 1.373 0.171 男女在大多数选项上没有显著差异，只有“价格价值”这一项的均值差异显著（P = 0.046），表明男性和女性在价格价值感知上存在显著差异。 这一发现标明性别在价格敏感度和价值认知方面有着重要作用。未来的研究可以进一步探索这一差异背后的原因，分析可能的社会文化因素或心理机制。同时，企业和品牌可以针对不同性别设计更加个性化的营销策略和活动方案，以提高针对性和市场竞争力。例如，男性和女性可能在价格优惠、促销活动的响应度上有所不同，因此定制化的价格策略可能有助于提升销售效果。 单因素方差分析（ANOVA） 维度 大一 大二 大三 大四 硕士 博士 F值 P值 绩效期望 3.79±0.87 3.66±0.85 3.49±0.82 3.62±0.93 3.77±0.58 4.17±0.88 0.873 0.5 努力期望 3.92±0.81 3.67±1.00 3.56±0.73 3.96±0.89 4.10±0.42 2.89±1.71 2.329 0.043 促进因素 3.90±0.77 3.61±0.91 3.16±0.84 3.65±1.00 4.08±0.58 4.11±0.77 4.28 0.001 社会影响 3.80±0.82 3.51±0.89 3.41±0.65 3.86±0.86 4.21±0.50 3.67±0.33 2.881 0.015 感知风险 3.79±0.82 3.66±0.94 3.48±0.86 3.91±0.84 4.13±0.83 4.11±1.02 1.534 0.18 享乐动机 3.81±0.83 3.47±0.98 3.32±0.81 3.66±0.86 3.77±0.58 3.67±1.15 2.171 0.058 价格价值 3.63±0.86 3.36±0.91 3.02±0.63 3.23±0.77 3.69±0.74 3.83±1.04 3.398 0.005 个体创新 3.95±0.77 3.59±0.93 3.57±0.65 3.90±0.85 4.03±0.78 3.89±1.02 2.304 0.045 使用意愿 3.69±0.82 3.48±0.92 3.07±0.89 3.48±0.78 4.10±0.69 4.00±1.00 3.745 0.003 在大多数维度中，不同年级和学术阶段的学生表现出显著差异，尤其在努力期望、促进因素、社会影响、价格价值、个体创新和使用意愿等方面，P值均小于0.05，表明这些因素受到年级和学术阶段的显著影响。 然而，绩效期望、感知风险和享乐动机的差异不显著（P>0.05），这些因素在不同年级和学术阶段之间的变化较小。 对显著的变量进行进一步分析。具体结果如下表（事后检验---LSD）所示 维度 I J 平均值差值 (I-J) 显著性 努力期望 博士研究生 大学一年级 -1.02778* 0.041 大学四年级 -1.07190* 0.039 硕士研究生 -1.21368* 0.028 促进因素 大学三年级 大学一年级 -0.74104* 0 大学二年级 -0.44920* 0.025 大学四年级 -0.48706* 0.028 硕士研究生 -0.91692* 0.001 社会影响 大学二年级 大学一年级 -0.29059* 0.025 大学四年级 -0.35125* 0.046 硕士研究生 -0.69363* 0.006 大学三年级 大学一年级 -0.38875* 0.029 大学四年级 -0.44941* 0.037 硕士研究生 -0.79179* 0.005 价格价值 大学一年级 大学二年级 0.26724* 0.045 大学三年级 0.60500* 0.001 大学四年级 0.39706* 0.015 大学三年级 硕士研究生 -0.67231* 0.019 个体创新 大学一年级 大学二年级 0.36171* 0.005 大学三年级 0.37458* 0.035 使用意愿 大学三年级 大学一年级 -0.62214* 0.001 大学二年级 -0.41034* 0.042 硕士研究生 -1.03590* 0 硕士研究生 大学二年级 0.62555* 0.016 大学三年级 1.03590* 0 大学四年级 0.62707* 0.023 努力期望：博士研究生与其他年级（大学一年级、大学四年级、硕士研究生）的有差异显著。 促进因素：大学三年级与其他年级（大学一年级、大学二年级、大学四年级、硕士研究生）之间的差异显著。尤其是与硕士研究生之间的差异最为显著（P=0.001）。 社会影响：大学二年级和大学一年级之间的差异显著，P值为0.025；大学三年级与大学一年级、大学四年级、硕士研究生之间的差异也显著，表明不同年级的学生在社会影响的感知上存在显著差异。 价格价值：大学一年级与大学二年级、大学三年级、大学四年级之间的差异显著，而大学三年级与硕士研究生之间的差异也具有显著性，表明年级的不同显著影响学生对价格价值的评价。 个体创新：大学一年级与大学二年级、大学三年级之间存在显著差异，表明学生的创新能力在不同年级之间有所不同。 使用意愿：大学三年级与大学一年级、大学二年级、硕士研究生之间存在显著差异，尤其是硕士研究生和大学三年级之间的差异最大，表明硕士研究生对使用意愿的评分远高于大学生。
-
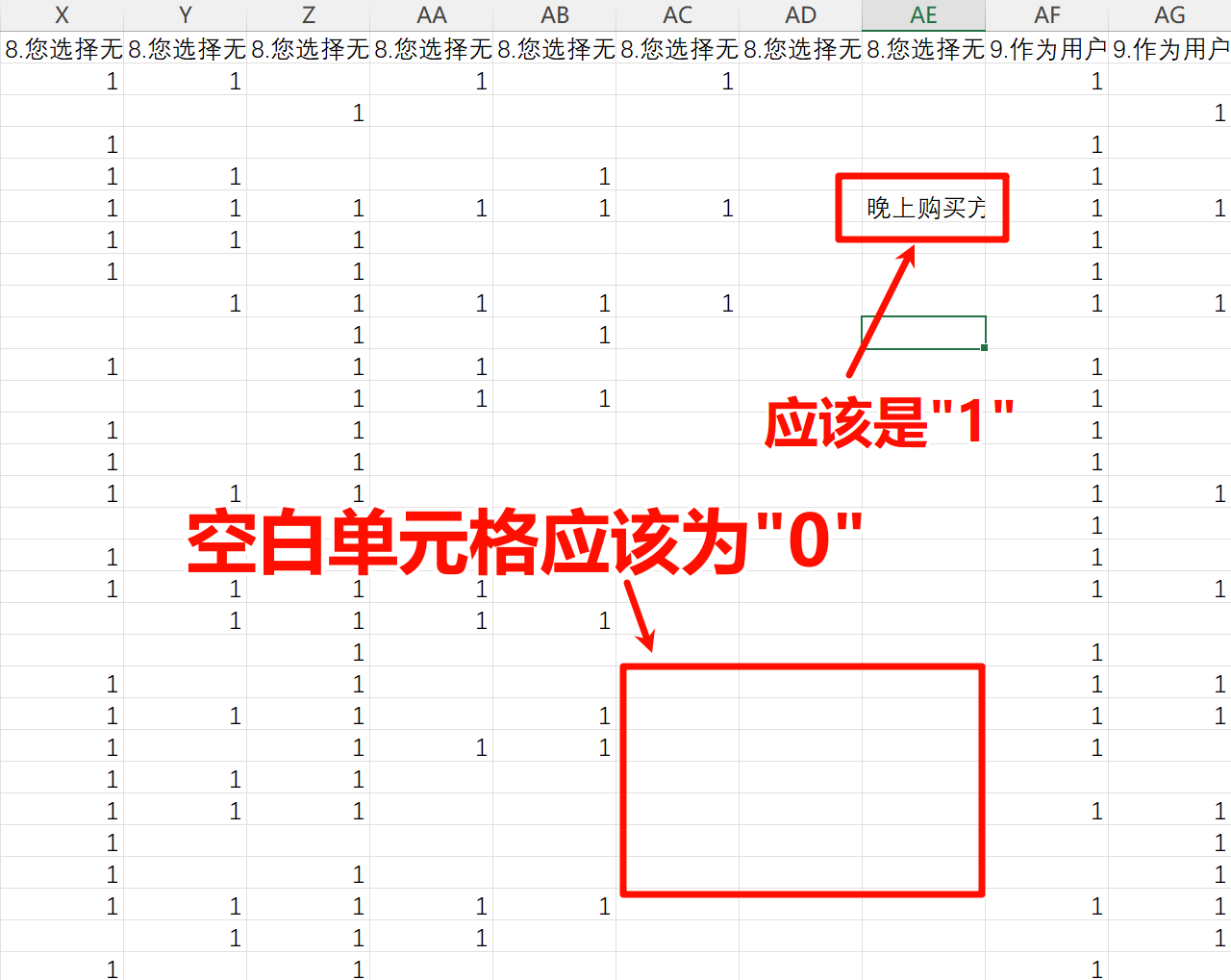
清洗数据---空值变成0 缘由 因为发现从腾讯问卷导出的数据，多选题格式不正确，不适合导入到SPSS里面做分析。问题主要有： 未选中应该是0，这里为空值。 其他列如果有应该为1，这里直接是填写后的内容。 问题展示： 因此，我通过 Python 代码进行了数据清洗。 使用前准备 重新命名变量：首先需要对变量进行重新命名，例如：Q1、Q2 等，针对多选题，命名为 Q3_1、Q3_2 等。变量名应为变量的英文缩写，例如：感知易用性可以命名为 PEOU1、PEOU2。 将 Excel 文件保存为 CSV 格式。操作步骤如下： 启动 Excel 并打开目标文件。 点击左上角的“文件”菜单。 在菜单中选择“另存为”（有些版本可能会直接显示“保存为”）。 在弹出的对话框中选择保存文件的位置。 在“保存类型”下拉框中选择 CSV（逗号分隔）（*.csv）。 这是已经准备完毕的数据格式示例： 确保 Python 已安装 numpy 和 pandas 库。如果没有，请在命令行终端输入以下命令： pip install numpy pip install pandas 复制文件路径 选中目标文件或文件夹。 按下 Ctrl + Shift + C，将文件或文件夹的完整路径复制到剪贴板。 注意：复制的路径会包含引号，后续需要去除引号。 代码 import pandas as pd # 读取 CSV 文件，将 'input.csv' 替换为你的文件路径，注意去除路径中的引号。 # 例如，若复制路径为 "C:\Users\xcyy5\Desktop\test.csv"，则应去掉引号，改为 C:\Users\xcyy5\Desktop\test.csv。 # 注意：代码中的单引号不要更改或删除 df = pd.read_csv(r'input.csv') # 定义需要处理的列范围（从 A 到 B），A 替换为多选题的第一题列名，B 替换为最后一题列名。 # 例如，若我的多选题从第六题到第八题，第八题有 4 个选项，A 替换为 Q6_1，B 替换为 Q8_4。 columns_to_process = df.loc[:, 'A':'B'].columns # 对指定列进行处理：非 1 的值（包括空值）替换为 0 df[columns_to_process] = df[columns_to_process].apply(lambda col: col.apply(lambda x: 1 if x == 1 else 0)) # 保存处理后的结果到新文件，确保汉字正确输出。将 'output.csv' 替换为导出文件的路径。 # 例如，如果想导出到 D 盘的 works 文件夹，并命名为“清洗后-空值为0.csv”，则路径为 D:\works\清洗后-空值为0.csv。 # 注意：代码中的单引号不要更改或删除 df.to_csv(r'output.csv', index=False, encoding='utf_8_sig') print("处理完成，文件已保存！")
