找到
33
篇与
她笑中藏泪花
相关的结果
- 第 6 页
-
【SPSS】正态检验 #BV# 如果视频不清晰请点此观看原视频 操作步骤 选择分析方法：在菜单栏中点击“分析”，然后选择“描述统计”，接着点击“探索”。 设置变量：将待检验的变量添加至“因变量列表”框中。 选择图形：点击“图”按钮，勾选“直方图”和“含检验的正态图”选项，然后点击“继续”。 运行分析：点击“确定”以启动分析过程。 结果解读 观察图 直方图：通过观察直方图的数据分布，判断其是否接近正态分布。正态分布通常表现为中间较高，两端较低的钟形曲线。 Q-Q图：检查Q-Q图中数据点的分布，确认它们是否沿对角线排列。若数据点接近对角线，则表明数据分布接近正态。 观察表 观察图只是一个简便的方法，严谨的应该是看表。 往下看，会有一个名为“正态性检验”的表。 我们主要看显著性，如果大于0.05证明数据符合正态分布；小于0.05则证明数据不符合正态分布。 表里一般有两种检验方式，一种是柯尔莫戈洛夫-斯米诺夫检验(Kolmogorov-Smirnov test)，简称K-S检验；夏皮洛-威尔克检验(Shapiro—Wilk test)，简称S-W检验。 这两个在适用性上不同，K-S检验适用于样本量大于50个的情况；S-W适用于样本量小于50个的情况。
-
【AI】使用Deepseek+通义千问或kimi快速制作可编辑的PPT #BV# 若视频不清晰可以点此观看原视频 介绍 最近，我发现了通义千问和Kimi上有一些非常实用的文本转PPT工具。我尝试了一下，效果不错，而且生成的PPT是可编辑的格式。结合Deepseek-R1（深度思考）生成文本的能力，效果更佳。 使用过程 Deepseek生成文本 首先打开DeepSeek ,选着深度思考(R1)，然后告诉它你想要生成的内容，最后加上“以markdown格式输出”的要求。 例如，如果我现在需要生成一个关于市场营销专业的汇报，我可以对Deepseek说：“请你扮演一名市场营销专业的大三学生，要对大一新生进行市场营销专业介绍，并分享一些学习经验。请你生成一份文案文本，且以markdown格式输出。”生成后，你可以对文案进行修改和调整，直至满意。 注：除了Deepseek，其他的AI模型也同样可以使用，效果同样不错。 AI生成PPT 接下来，打开通义千问或者Kimi，这两个工具都非常实用。相对而言，Kimi的模板种类更多，还能生成一些AI图片；而通义千问生成的PPT则显得更简洁大气，个人认为设计感更强。 通义千问操作步骤： 打开通义千问，选择“效率”—“工具箱”—“PPT创作”。 选择“长文本生成PPT”并将Deepseek生成的文案粘贴到这里。 按需调整文案，并选择演讲场景，继续下一步。 选择一个适合的模板，生成PPT。 进行微调，调整完成后，点击右上角的“导出”，选择“导出为PPT”。 Kimi操作步骤： 打开Kimi，点击“Kimi+”进入“PPT助手”。 将文本粘贴到输入框，点击“一键生成PPT”。 选择模板，生成PPT。 进入编辑界面进行微调，最后下载PPT，文字仍然可以编辑。 写在最后 利用AI大模型生成PPT是一种高效的方法。AI可以将文本很好地套用到PPT模板中，但生成的结果仍有改进空间。 建议大家先自己编写文案，再让AI大模型帮忙润色并转换成Markdown格式。生成PPT后，还可以根据需要插入一些图表来丰富内容，提升PPT的视觉效果。
-
【SPSS】效度分析 #BV# 不清晰可点此观看原视频：【spss】效度分析---探索性因子分析和主成分分析_哔哩哔哩_bilibili 三类 效度分析主要分为探索性因子分析(EFA) 、主成分分析(PCA)、 验证性因子分析(CFA) 探索性因子分析（EFA）---SPSS 探索性因子分析（EFA）用于在缺乏明确假设的情况下，探索数据中的潜在因子结构。其主要目的是识别影响观测变量的潜在因子数量，并揭示各因子与观测变量之间的关系。EFA通常用于研究的初步阶段，帮助研究者理解数据的内在结构，并为后续的理论构建或假设生成提供基础。 主成分分析(PCA)---SPSS 主成分分析（PCA）是一种常用的数据降维方法，旨在通过线性变换将原始的高维数据转化为一组不相关的新变量，即主成分。PCA通常用于探索变量背后的潜在因子，特别是在数据结构不明确的情况下，例如开发新的量表时。 验证性因子分析（CFA）---AMOS 验证性因子分析（CFA）用于验证研究者预设的因子结构模型是否与实际数据相符。在CFA中，研究者需要明确假设因子的数量、因子之间的相关性以及各观测变量与因子之间的关系。CFA通常用于理论验证阶段，检验量表或模型的结构效度。 步骤 计算KMO值 步骤： 打开SPSS并导入数据：启动SPSS，点击“文件” > “打开” > “数据”，选择你的数据文件。 选择因子分析：点击“分析” > “降维” > “因子”。 选择变量：在弹出的对话框中，将需要分析的变量添加到“变量”框中。 设置描述统计：点击“描述”按钮，勾选“系数”和“KMO和巴特利特球形度检验”，然后点击“继续”。 运行分析：点击“确定”以运行分析。 进行主成分分析 步骤： 选择因子分析：点击“分析” > “降维” > “因子”。 选择变量：在弹出的对话框中，将需要分析的变量添加到“变量”框中。 设置描述统计：点击“描述”按钮，勾选“系数”和“KMO和巴特利特球形度检验”，然后点击“继续”。 设置提取方法：点击“提取”按钮，选择“主成分”作为提取方法。 设置旋转方法：点击“旋转”按钮，选择“最大方差法”作为旋转方法。 选项：勾选“取消小系数”按钮，填入：“0.4”（具体填入多少根据因子载荷量标准决定）。 运行分析：点击“确定”以运行分析。 概念解释与结果解读 KMO和巴特利特球形度检验 KMO值 低于 0.5 表示不适合因子分析，0.5–0.7 较为一般，0.7–0.8 较好，0.8–0.9 非常好，0.9 以上则非常适合 Bartlett, M. S. (1950). “Tests of significance in factor analysis.” British Journal of Mathematical and Statistical Psychology, 3(2), 77–85. 显著性 当检验的显著性水平小于 0.05 时，可以拒绝“单位矩阵”假设，认为数据适合进行因子分析。 可做成如下表所示： 维度 信度 效度 维度1 xx xx 维度2 xx xx 维度3 xx xx 总体 xx xx 主成分分析 是不是都要做？ 并非所有量表都必须进行主成分分析（PCA）。在实际研究中，许多论文只进行了KMO检验： 研究目的不同： 如果研究的主要目的是评估量表的信度或其他指标，而非探索潜在因子结构，可能只进行KMO检验。 数据特性： 如果量表的题项数量较少，或者题项之间的相关性较弱，可能不适合进行主成分分析。 研究领域惯例： 在某些研究领域，可能更倾向于使用其他方法来评估量表的效度，而非主成分分析。 使用的是成熟的量表： 研究使用的是已经被广泛验证和使用的成熟量表（如广泛应用的心理学量表、教育测量量表等），并且这些量表的效度和信度已经得到充分证明，那么可能不需要重复进行效度分析。在这种情况下，直接引用这些量表的效度分析结果。 预调查或先行研究： 在某些研究中，可能会在正式研究之前进行预调查或先行研究，以测试量表的效度和信度。如果预调查的结果显示量表有效且信度高，研究者可能会选择不再进行全面的效度分析，尤其是在量表已经经过充分验证的情况下。 关键概念解释 共同度： 衡量了一个变量的方差中有多少比例可以被提取的因子解释。 如果一个变量的共同度较低，意味着它包含了较多无法通过因子分析解释的独特信息，可能需要考虑删除该变量。 一般要求是大于0.4 因子载荷系数： 表示每个变量与各个因子之间的相关程度。 要求为：0.5、0.45、0.35都有，一般认为0.4。 绝对值大于0.4被认为是显著的，意味着该变量与对应的因子有较强的关联。 绝对值小于0.4，可能表示该变量与因子的关联较弱，建议考虑删除或重新评估该变量。 方差解释率和累积方差解释率: 方差解释率：表示每个因子或主成分所解释的方差占总方差的比例。 累积方差解释率：则是前n个因子或主成分的方差解释率之和。例如，如果前两个因子的方差解释率分别为75%和15%，则累积方差解释率为90%，意味着这两个因子共同解释了原始数据90%的方差。 ＞50%即可 效度不达标怎么办？ 处理异常数据： 检查并剔除答题时间过短（如低于60秒）或回答重复度过高的问卷，以确保数据质量。 删除低质量题项： 识别并删除低共同度题项：在因子分析中，共同度值低于0.4的题项应删除，以提高因子分析的有效性。 评估题项有效性：删除那些与在其他题项下面或因子载荷系数低于0.4的题项，从而提高量表的内部一致性。 与对应维度出现严重偏差（张冠李戴）。 提取---勾选“因子的固定数目（N）”---要提取的因子数(I) 输入你的维度数，强行提取因子分析。
-
【spss】信度分析 #BV# 如果不清晰请点此处观看原视频：【spss】信度分析---可靠性检验_哔哩哔哩_bilibili 步骤 分析---刻度---可靠性分析 把量表题目拖入进去(先单个维度、再总体) 统计---勾选“描述”下的“删除项后的标度” 继续---确定 最终表格绘制如下： 概念解释与结果解读 克隆巴赫Alpha 定义：克隆巴赫Alpha（Cronbach’s α）是衡量量表内部一致性的常用指标。 标准： α ≥ 0.9：好 0.9＞α ≥ 0.8：良好 0.8＞α ≥ 0.7：可以接受 0.7＞ α ≥ 0.6：仍具有一定的信度，但需谨慎解释 0.6＞ α：信度不足，建议修改或删除部分题项 Agbo A A. Cronbach’s Alpha: Review of Limitations and Associated Recommendations[J]. Journal of Psychology in Africa, 2010, 20(2): 233-239. 若删除某一题项后Alpha值升高 可直接删除这个题目再进行分析 检查问卷，剔除答题时间过短以及回答重复过多等无效问卷 删除后Alpha值提升幅度较小（如+0.05）则保留 进行探索性因子分析(EFA)，共同度或因子载荷符合标准（共同度＞0.3，载荷>0.4）则保留 可做成以下表格样式： 维度 信度 效度 维度1 xx xx 维度2 xx xx 维度3 xx xx 总体 xx xx
-
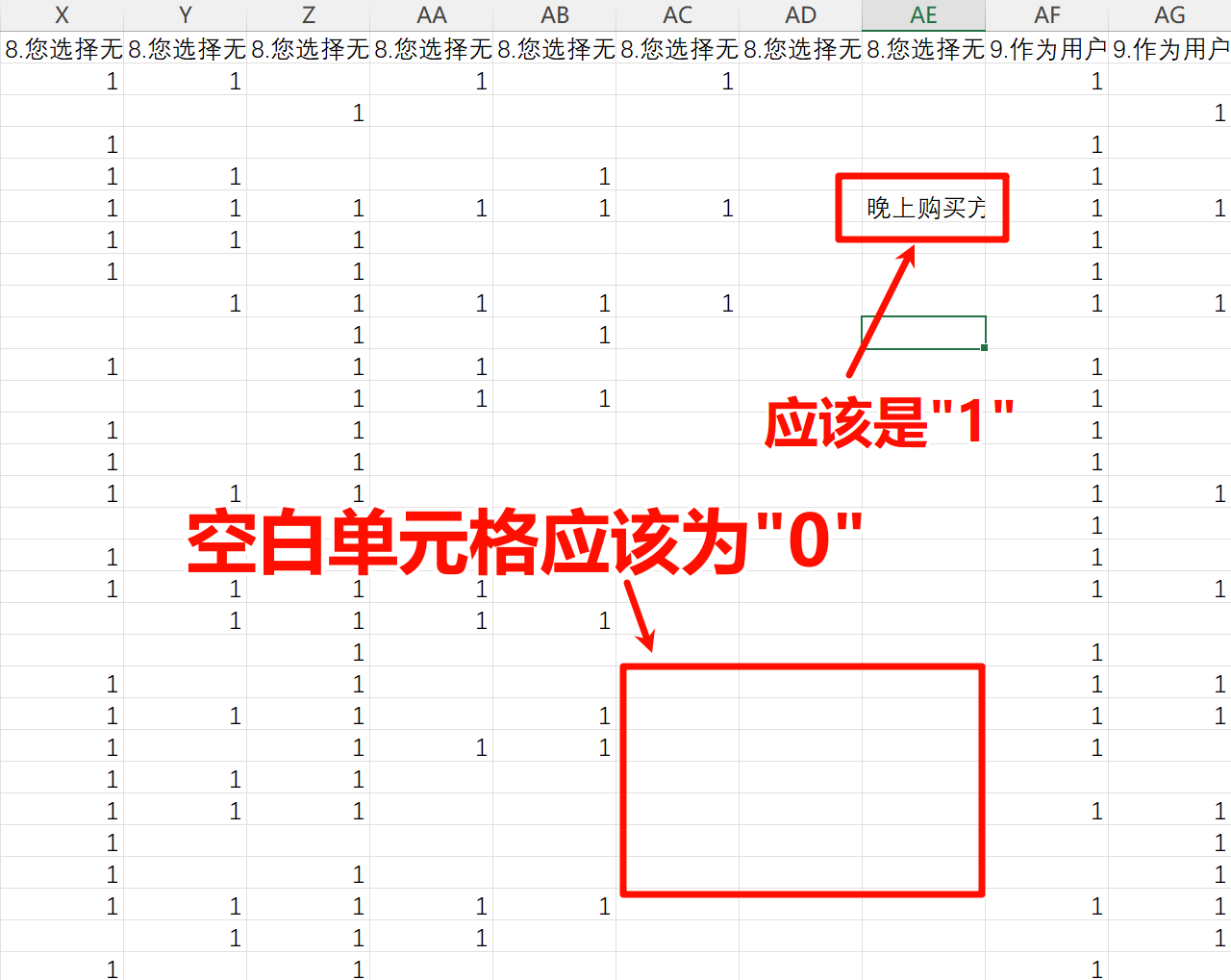
清洗数据---空值变成0 缘由 因为发现从腾讯问卷导出的数据，多选题格式不正确，不适合导入到SPSS里面做分析。问题主要有： 未选中应该是0，这里为空值。 其他列如果有应该为1，这里直接是填写后的内容。 问题展示： 因此，我通过 Python 代码进行了数据清洗。 使用前准备 重新命名变量：首先需要对变量进行重新命名，例如：Q1、Q2 等，针对多选题，命名为 Q3_1、Q3_2 等。变量名应为变量的英文缩写，例如：感知易用性可以命名为 PEOU1、PEOU2。 将 Excel 文件保存为 CSV 格式。操作步骤如下： 启动 Excel 并打开目标文件。 点击左上角的“文件”菜单。 在菜单中选择“另存为”（有些版本可能会直接显示“保存为”）。 在弹出的对话框中选择保存文件的位置。 在“保存类型”下拉框中选择 CSV（逗号分隔）（*.csv）。 这是已经准备完毕的数据格式示例： 确保 Python 已安装 numpy 和 pandas 库。如果没有，请在命令行终端输入以下命令： pip install numpy pip install pandas 复制文件路径 选中目标文件或文件夹。 按下 Ctrl + Shift + C，将文件或文件夹的完整路径复制到剪贴板。 注意：复制的路径会包含引号，后续需要去除引号。 代码 import pandas as pd # 读取 CSV 文件，将 'input.csv' 替换为你的文件路径，注意去除路径中的引号。 # 例如，若复制路径为 "C:\Users\xcyy5\Desktop\test.csv"，则应去掉引号，改为 C:\Users\xcyy5\Desktop\test.csv。 # 注意：代码中的单引号不要更改或删除 df = pd.read_csv(r'input.csv') # 定义需要处理的列范围（从 A 到 B），A 替换为多选题的第一题列名，B 替换为最后一题列名。 # 例如，若我的多选题从第六题到第八题，第八题有 4 个选项，A 替换为 Q6_1，B 替换为 Q8_4。 columns_to_process = df.loc[:, 'A':'B'].columns # 对指定列进行处理：非 1 的值（包括空值）替换为 0 df[columns_to_process] = df[columns_to_process].apply(lambda col: col.apply(lambda x: 1 if x == 1 else 0)) # 保存处理后的结果到新文件，确保汉字正确输出。将 'output.csv' 替换为导出文件的路径。 # 例如，如果想导出到 D 盘的 works 文件夹，并命名为“清洗后-空值为0.csv”，则路径为 D:\works\清洗后-空值为0.csv。 # 注意：代码中的单引号不要更改或删除 df.to_csv(r'output.csv', index=False, encoding='utf_8_sig') print("处理完成，文件已保存！")
